Test Methods
Mechanical Properties of Plastics
-
STRESSOpen or Close
How does one know if a material will be strong enough for a part? If the loads can be predicted and the part shape is known then the designer can estimate the worst load per unit of cross-sectional area within the part. Load per unit area is called "STRESS".
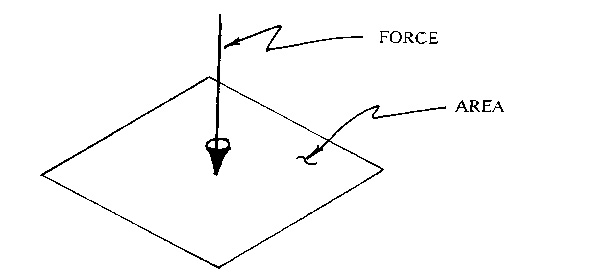
-
STIFFNESS (Modulus)Open or Close
Sometimes a designer knows a part can only bend or deflect a certain amount. If the maximum amount of bending and the shape of the part are known, then the designer can often predict how STIFF a material must be. The measurement of the STIFFNESS of a material is called the "MODULUS" or "MODULUS OF ELASTICITY." The higher the modulus number, the stiffer the material; and conversely, the lower the number, the more flexible the material. The Modulus also changes as the temperature changes
-
STRAINOpen or Close
The measurement of how much the part bends or changes size under load compared to the original dimension or shape is called "STRAIN." Strain applies to small changes in size.
STRAIN = (Final Length - Original Length)/Original Length= Change in Length or Deformation/Original Length
STRESS, STRAIN, and MODULUS are related to each other by the following equation. The modulus or stiffness of a material can be determined when the material is loaded in different ways, such as tension, compression, shear, flexural (bending) or torsion (twisting). They will be called TENSILE MODULUS, also known as plain MODULUS, FLEXURAL MODULUS, TORSIONAL MODULUS, etc.
MODULUS = STRESS/STRAIN or, in other words
MODULUS = Load /change in shape when loaded. (STIFFNESS)
Choose the type of modulus in the property sheet that most nearly duplicates what the customer expects the major load to be, tension, bending (flexural). If the load is unknown, use the lowest module value of the two. These numbers can be used for short-term loading if the load is to be applied for only a few days at the most.
The stress/strain equation is the equation used by designers to predict how a part will distort or change size and shape when loaded. Predicting the stress and strain within an actual part can become very complex. Fortunately, the material suppliers use tests that are easy to understand.
THE PERFORMANCE OF A PLASTIC PART IS AFFECTED BY:
- What kind of load the part will see (Tensile, Impact, Fatigue, etc.)
- How big the load is
- How long or often that load will be applied
- How high and/or low a temperature the part will see
- How long it will see those temperatures
- The kind of environment the part will be used in. Will moisture or other chemicals be present?
This is where plastics differ in their behaviour when compared to other materials, such as metals and ceramics. Choosing stress and/or moduli values that are too high and do not account for the time and temperature effects can lead to failure of the part.
-
YIELD POINTOpen or Close
The yield point is that point when a material subjected to a load, tensile, compressive, etc. gives (yields) and will no longer return to its original length or shape when the load is removed. Some materials break before reaching a yield point, for example, some glass-filled nylons or die cast aluminium.
To try to further visualize this property, take a piece of wire and slightly bend it. It will return to its original shape when released. Continue to bend and release the wire further and further. Finally the wire will bend and not return to its original shape. The point at which it stays bent is the "YIELD POINT." The "yield point" is a very important concept because a part is usually useless after the material has reached that point.
-
TENSILE STRENGTHOpen or Close
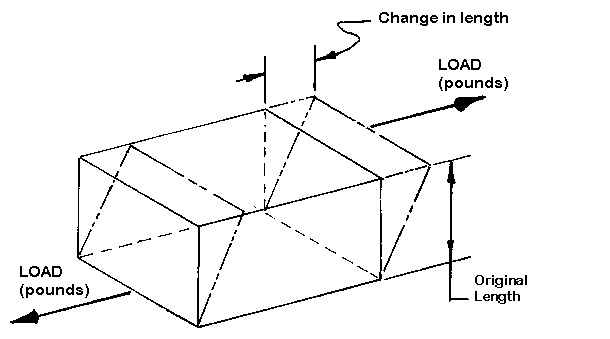
The maximum strength of a material without breaking when the load is trying to pull it apart is shown in Figure 4. This is the system used by the suppliers to report tensile properties in their literature, such as strength and elongation.
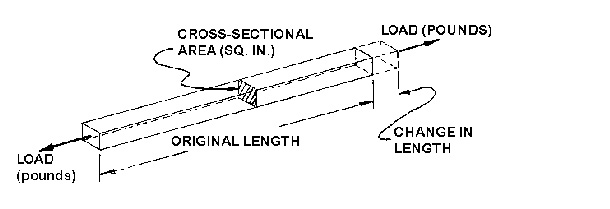 <br>
<br>A good way to visualize this property is to think of pulling a fresh marshmallow apart and then pulling a piece of taffy apart. The force or pounds required to pull the taffy apart would be much greater than required to pull the marshmallow apart. If that force is measured and the taffy and marshmallow each had a cross-sectional area of one square inch, then the taffy has the higher "tensile strength" in terms of pounds per square inch. Plastics may demonstrate tensile strengths from 1000 psi (pounds per square inch) to 50,000 psi.
-
ELONGATIONOpen or Close
Elongation is always associated with tensile strength because it is the increase in the original length at fracture and expressed as a percentage. An example would be to pull on a 1 " wide piece of paper that is 4" long. It tears with no visible elongation or nearly 0% elongation. Now do the same thing to a 1" x 4" piece of taffy. It will stretch several times its original 4" length before it fractures. Assume that it is stretched to a 12" length then (12"/4") (100) = 300% elongation.
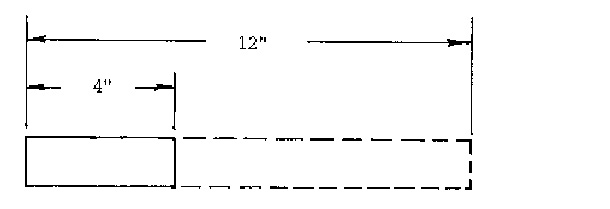
-
COMPRESSIVE STRENGTHOpen or Close
The maximum strength of a material without breaking when the material is loaded as shown in Figure 6. Check if the material supplier has the information on compressive strength, since it is not always determined.
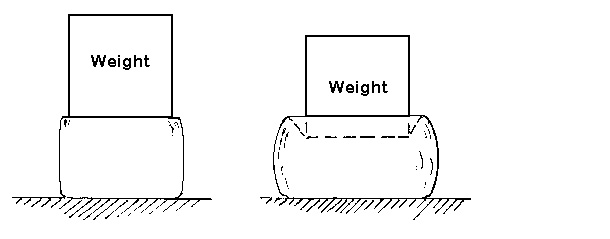
This term becomes less meaningful with some of the softer materials. PTFE, for example, does not fracture. Consequently, the compressive strength continues to increase as the sample is deforming more and more. A meaningful "compressive strength" would be the maximum force required to deform a material prior to reaching the yield point. The compressive term similar to "elongation" is "compressive deformation," though it is not a commonly reported term. It is easy to visualize two identical weights (FIGURE 7), one sitting on a 1" cube of fresh marshmallow and the other on a 1" cube of taffy. The marshmallow would be flattened and deformed more.
-
SHEAR STRENGTHOpen or Close
The strength of a material when the material is loaded as shown in Figure 8. The surfaces of the material are being pulled in opposite directions. Some examples of items that see shear loading are the nail holding a picture on the wall, the cleats of athletic shoes, and tire tread as a car speeds up or slows down.
-
FLEXURAL STRENGTHOpen or Close
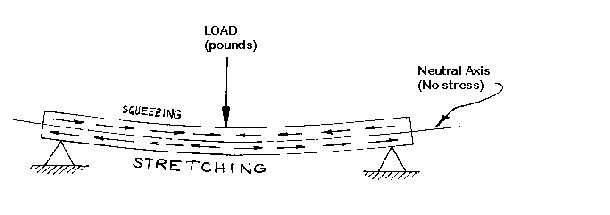
The strength of a material when a beam of the material is subjected to bending as shown in Figure 9. The material in the top of the beam is in compression (squeezed together), while the bottom of the beam is in tension (stretched). Somewhere in between the stretching and squeezing there is a place with no stress and it is called the neutral plane. A simple beam supported at each end and loaded in the middle is used to determine the flexural modulus given in properties tables. Skis, a fishing pole, a pole vault pole, and a diving board are examples of parts needing high flexural strength.
-
TORSIONAL STRENGTHOpen or Close
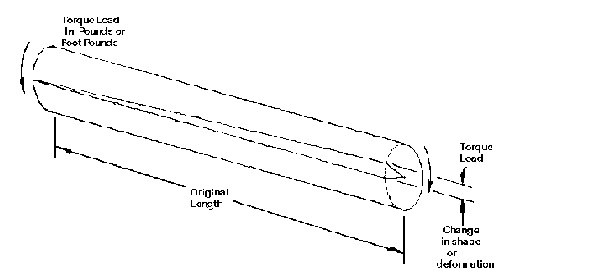
The strength of a material when a shape is subjected to a twisting load as shown in Figure 10. An example of a part with a torsion load is a screw as it is being screwed in. The drive shaft on a car also requires high torsional strength.
-
CREEPOpen or Close
Visualise large weights being hung on bars of different materials. All materials will experience some initial and immediate deformation or stretching when the load is first applied. As long as the yield point has not been exceeded, a metal sample which acts like a spring will not stretch any more regardless of how long the weight is left on. When the weight is removed, the metal bar will return to its original shape. The length of a "thermoplastic" bar will continue to slowly increase as long as the load is applied. This is called CREEP. The amount of creep increases as the load and/or temperature are increased. Some thermoplastics like nylons will creep more when they have softened because of the presence of moisture. The "crosslinked" or "3D net" structure in "thermosets" resists creep better than thermoplastics. Reinforcements like glass and carbon, which do not creep, greatly reduce the creep of the composite material when mixed with a plastic.
Remember the relationship between stress/strain/modulus is:
Modulus = Stress/Strain
The initial strain or change in length with the weight will give a value for the modulus (this is usually the short term value reported in the property tables for the tensile modulus or flexural modulus). If the weight (stress) is left on over a period of time, the amount of bending or elongation continues to increase and the value for the modulus will decrease with time as shown in Figure 16. This decreasing modulus that is a function of time (and even temperature) is called the "CREEP MODULUS" or "APPARENT MODULUS."
This is the modulus that the designer should be using to more accurately predict the behaviour of the plastic materials. The value chosen from the supplier's literature will be based on the estimated time the load will be applied, the amount of the load, and the temperature conditions present when the load is to be applied.
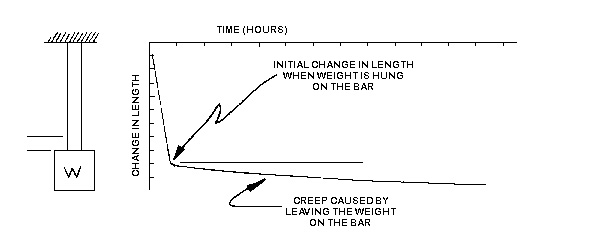
Remember that creep is affected by:
- Load (stress)
- Temperature
- Length of time the load is applied
- Other environmentals, such as moisture or chemicals
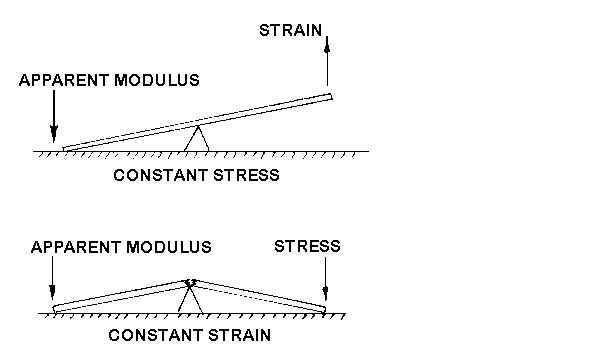
Since the STRESS is kept constant, ie., the weight or load is not changed or removed, the equation becomes:
Apparent Modulus x Total Strain = Constant (Stress)
Or in other words, if the strain goes up, then the Apparent Modulus must come down. Since the strain increases with time and temperature, the Apparent Modulus decreases with time and temperature. The data is sometimes presented in supplier literature in terms of Stress Relaxation. This means that the STRAIN is held constant and the decrease in the load (stress) is measured over time. This is called "STRESS RELAXATION''. This information is important for applications, such as gaskets, snap fits, press fits, and parts joined with screws or bolts. The equation becomes:
Apparent Modulus / Stress = Constant (Strain)
Or in other words, as the stress goes down because the material moves, then the apparent modulus also goes down.
Sometimes a supplier will recommend a maximum design stress. This has a similar effect to using the apparent modulus. The recommended design stress for some acrylic injection moulded parts is 500 psi and yet its tensile strength could be reported to be as much as 10,000 psi in the property chart. Designers will often look at the 10,000 psi value and cut it in half to be safe; however, it is not really enough and could lead to failure of the part.
-
FATIGUE STRENGTHOpen or Close
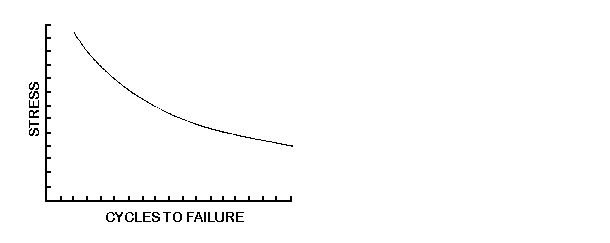
Plastics, as well as other materials, subjected to cyclic loading will fail at stress levels well below their tensile or compressive strengths. The combination of tension and compression is the most severe condition. This information will be presented in S-N Curves or tables. The S-N stand for Stress-Number of cycles. A PART WILL SURVIVE MORE CYCLES IF THE STRESS IS REDUCED. The stress can be reduced by reducing the deflection and/or decreasing the thickness of a part.
Some examples of cyclic loading are a motor valve spring or a washing machine agitator. With time, parts under cyclic loading will fail; however, properly designed and tested they will not fail before several million loadings have been completed. Figure 24 shows a typical S-N curve.
-
IMPACT STRENGTHOpen or Close
Many plastics demonstrate excellent impact strength. Impact strength is the ability to withstand a suddenly applied load. Toughness is usually used to describe the material's ability to withstand an impact or sudden deformation without breaking. No single test has yet been devised that can predict the impact behaviour of a plastic material under the variety of conditions to which a part can be subjected. Many materials display reduced impact strength as the temperature is lowered. Thermosets and reinforced thermoplastics may change less with changes in temperature. Check the supplier literature for any unusual factors that may affect the impact performance of a part.
Some of the impact tests commonly used in supplier literature are:
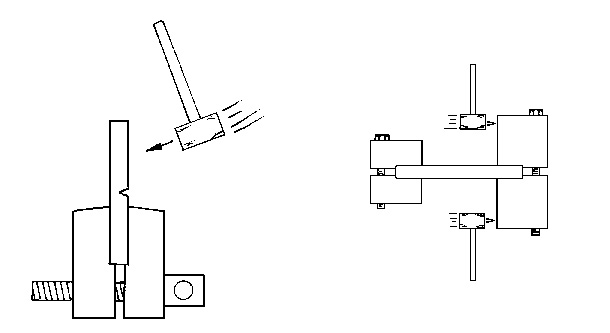
- Izod Test: designed to measure the effect of a sharp notch on toughness when the test specimen is suddenly impacted.
- Tensile Impact Test: designed to measure the toughness of a small specimen without a notch when subjected to a sudden tensile stress or load.
- Gardner Impact Test: drops a shaped weight and determines the energy required to break the test sample.
- Brittleness Temperature Test: determines ability of the material to continue to absorb impacts as the temperature is decreased.
Special tests may need to be devised to more nearly duplicate the actual application.
INFORMATION PROVIDED BY THESE TESTS WILL AID IN CHOOSING MATERIAL CANDIDATES; HOWEVER, THE DESIGNER MUST STILL TEST THE ACTUAL PART UNDER CONDITIONS AS NEAR AS POSSIBLE TO ACTUAL USE CONDITIONS BEFORE BEING CONFIDENT THAT THE MATERIAL SELECTION IS ADEQUATE.
-
NOTCH SENSITIVITYOpen or Close
Some plastic materials have exceptional impact performance and very good load carrying capability; however, the performance of a material can be greatly reduced by having sharp corners on the part. The sharp corners can be part of the design or from machining operations. A SHARP CORNER IS A GREAT PLACE FOR A CRACK TO START. The Izod impact strength of a tough material like polycarbonate is reduced from 20 to 2 as the radius of the notch is reduced from 0.020"R to 0.005"R respectively.
The sharp corners not only reduce the impact resistance of a part, but also allow for a stress concentration to occur and encourage the premature failure of a load carrying part.
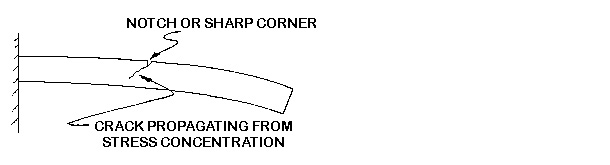
MINIMIZING SHARP CORNERS MAY MAKE THE MACHINING OPERATION MORE DIFFICULT; HOWEVER, IT MAY BE CRUCIAL TO THE PART'S SUCCESS.
Edges of sheet being used in impact applications like glazing must also be finished to be free of sharp notches. This is a concern with acrylics and even tough materials like polycarbonate.






